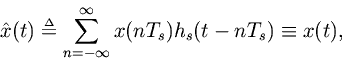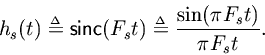06. Theory of Ideal Bandlimited Interpolation

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "The Digital Audio Resampling Home Page", by Julius O. Smith III, Copyright © 2016-05-17 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC Next page >>

Theory of Ideal Bandlimited Interpolation

We review briefly the ``analog interpretation'' of sampling rate conversion[Crochiere and Rabiner 1983] on which the present method is based. Suppose we have samples of a continuous absolutely integrable signal , where is time in seconds (real), ranges over the integers, and is the sampling period. We assume is bandlimited to $$\$ , where is the sampling rate. If $$X(\$ denotes the Fourier transform of , i.e., $$X(\$ , then we assume $$X(\$ for $$\$ . Consequently, Shannon's sampling theorem gives us that can be uniquely reconstructed from the samples via

(1)

where

To resample at a new sampling rate $$F_s^\$ , we need only evaluate Eq. (1) at integer multiples of $$T_s^\$ .
When the new sampling rate $$F_s^\$ is less than the original rate , the lowpass cutoff must be placed below half the new lower sampling rate. Thus, in the case of an ideal lowpass, $$h_s(t) = \$ , where the scale factor maintains unity gain in the passband.

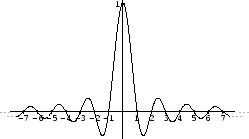
A plot of the sinc function $$\$ to the left and right of the origin is shown in Fig. 1. Note that peak is at amplitude , and zero-crossings occur at all nonzero integers. The sinc function can be seen as a hyperbolically weighted sine function with its zero at the origin canceled out.

Figure 1:The sinc function plotted for seven zero-crossings to the left and right.

If `` $$\$ '' denotes the convolution operation for digital signals, then the summation in Eq. (1) can be written as $$(x\$ .

Equation Eq. (1) can be interpreted as a superpositon of shifted and scaled sinc functions . A sinc function instance is translated to each signal sample and scaled by that sample, and the instances are all added together. Note that zero-crossings of $$\$ occur at all integers except . That means at time, (i.e., on a sample instant), the only contribution to the sum is the single sample . All other samples contribute sinc functions which have a zero-crossing at time . Thus, the interpolation goes precisely through the existing samples, as it should.

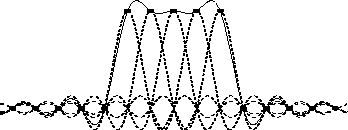
A plot indicating how sinc functions sum together to reconstruct bandlimited signals is shown in Fig. 2. The figure shows a superposition of five sinc functions, each at unit amplitude, and displaced by one-sample intervals. These sinc functions would be used to reconstruct the bandlimited interpolation of the discrete-time signal $$x = [\$ . Note that at each sampling instant , the solid line passes exactly through the tip of the sinc function for that sample; this is just a restatement of the fact that the interpolation passes through the existing samples. Since the nonzero samples of the digital signal are all , we might expect the interpolated signal to be very close to over the nonzero interval; however, this is far from being the case. The deviation from unity between samples can be thought of as ``overshoot'' or ``ringing'' of the lowpass filter which cuts off at half the sampling rate, or it can be considered a ``Gibbs phenomenon'' associated with bandlimiting.

Figure 2:Bandlimited reconstruction of the signal from its samples $$x = [\$ . The dots show the signal samples, the dashed lines show the component sinc functions, and the solid line shows the unique bandlimited reconstruction from the samples obtained by summing the component sinc functions.

A second interpretation of Eq. (1) is as follows: to obtain the interpolation at time , shift the signal samples under one sinc function so that time in the signal is translated under the peak of the sinc function, then create the output as a linear combination of signal samples where the coefficient of each signal sample is given by the value of the sinc function at the location of each sample. That this interpretation is equivalent to the first can be seen as a result of the fact that convolution is commutative; in the first interpretation, all signal samples are used to form a linear combination of shifted sinc functions, while in the second interpretation, samples from one sinc function are used to form a linear combination of samples of the shifted input signal. The practical bandlimited interpolation algorithm presented below is based on the second interpretation.