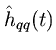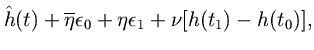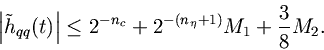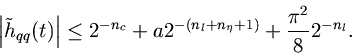11. Choice of Interpolation Resolution

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "The Digital Audio Resampling Home Page", by Julius O. Smith III, Copyright © 2016-05-17 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  Next page >>

Choice of Interpolation Resolution

We now consider the error due to finite precision in the linear interpolation between stored filter coefficients. We will find that the number of bits in the interpolation factor should be about half the filter coefficient word-length .

Quantized Interpolation Error Bound.

The quantized interpolation factor and its complement are representable as

			(10)
			(11)

where, since are unsigned, . The interpolated coefficient look-up then gives

			(12)
			(13)

where second-order errors and are dropped. Since , we obtain the error bound

The three terms in Eq. (2.6.2) are caused by coefficient quantization, interpolation quantization, and linear-approximation error, respectively.

Ideal Lowpass Filter.

For the ideal lowpass, the error bound is

Let and require that the added error is at most . Then we arrive at the requirement

<< Previous page  TOC  Next page >>