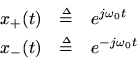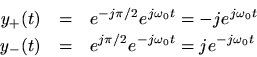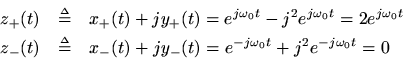The Analytic Signal and Hilbert Transform Filters

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. The Analytic Signal and Hilbert Transform Filters

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

The Analytic Signal and Hilbert Transform Filters

A signal which has no negative-frequency components is called ananalytic signal.5.6 Therefore, in continuous time, every analytic signal $z(t)$ can be represented as

\

where $Z(\ is the complex coefficient (setting the amplitude and phase) of the positive-freqency complex sinusoid $\ atfrequency $\.

Any sinusoid $A\ in real life may be converted to a positive-frequency complex sinusoid $A\ by simply generating a phase-quadrature component $A\ to serve as the ''imaginary part'':

\

The phase-quadrature component can be generated from the in-phase componentby a simple quarter-cycle time shift.5.7

For more complicated signals which are expressible as a sum of many sinusoids, a filter can be constructed which shifts each sinusoidal component by a quarter cycle. This is called a Hilbert transform filter. Let ${\ denote the output at time $t$ of theHilbert-transform filter applied to the signal $x(\. Ideally, this filter has magnitude $1$ at all frequencies and introduces a phase shift of$-\ at each positive frequency and $+\ at each negative frequency. When a real signal $x(t)$ and its Hilbert transform $y(t) = {\ are used to form a new complex signal $z(t) = x(t) + j y(t)$, the signal $z(t)$ is the (complex) analytic signal corresponding to the real signal $x(t)$. In other words, for any real signal $x(t)$, the corresponding analytic signal $z(t)=x(t) + j {\ has the property that all ''negative frequencies'' of $x(t)$ have been ''filtered out.''

To see how this works, recall that these phase shifts can be impressed on a complex sinusoid by multiplying it by $\. Consider the positive and negative frequency components at the particular frequency$\:

\



Now let's apply a $-90$ degrees phase shift to the positive-frequency component, and a $+90$ degrees phase shift to the negative-frequency component:

\



Adding them together gives

\



and sure enough, the negative frequency component is filtered out. (There is also a gain of 2 at positive frequencies which we can remove by defining the Hilbert transform filter to have magnitude 1/2 at all frequencies.)

For a concrete example, let's start with the real sinusoid

\

Applying the ideal phase shifts, the Hilbert transform is

\

The analytic signal is then

\

by Euler's identity. Thus, in the sum $x(t) + j y(t)$, the negative-frequency components of $x(t)$ and $jy(t)$ cancel out in the sum, leaving only the positive-frequency component. This happens for any real signal $x(t)$, not just for sinusoids as in our example.

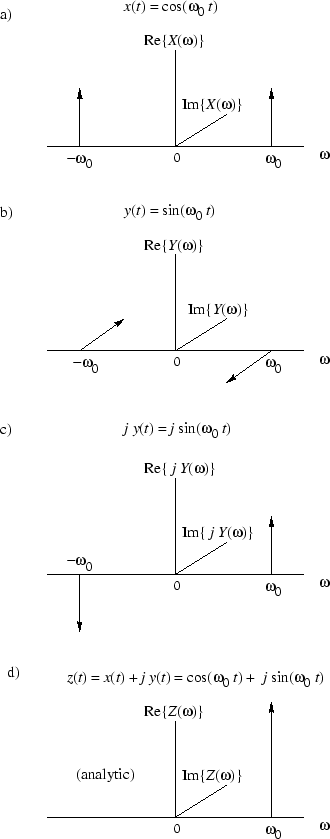
Figure 5.8:Creation of the analytic signal $z(t)=e^{j\ from the real sinusoid $x(t) = \ and the derived phase-quadrature sinusoid $y(t) = \, viewed in the frequency domain. a) Spectrum of $x$. b) Spectrum of $y$. c) Spectrum of $j y$. d) Spectrum of $z = x + jy$.
\

Figure 5.8 illustrates what is going on in the frequency domain. While we haven't ''had'' Fourier analysis yet, it should come as no surprise that the spectrum of a complex sinusoid $\ will consist of a single ''spike'' at the frequency $\ and zero at all other frequencies. (Just follow things intuitively for now, and revisit Fig. 5.8 after we've developed the Fourier theorems.) From the identity $2\, we see that the spectrum contains unit-amplitude ''spikes'' at $\ and $\. Similarly, the identity $2\ says that we have an amplitude$-j$ spike at $\ and an amplitude $+j$ spike at $\. Multiplying $y(t)$ by $j$ results in $j\ which is a unit-amplitude ''up spike'' at $\ and a unit ''down spike'' at $\. Finally, adding together the first and third plots, corresponding to $z(t) = x(t) + j y(t)$, we see that the two up-spikesadd in phase to give an amplitude 2 up-spike (which is $2\), and the negative-frequency up-spike in the cosine iscanceled by the down-spike in $j$ times sine at frequency$-\. This sequence of operations illustrates how the negative-frequency component $\ gets filtered outby the addition of $2\ and $j 2\.

As a final example (and application), let $x(t) = A(t)\, where $A(t)$ is a slowly varying amplitude envelope (slow compared with$\). This is an example of amplitude modulation applied to a sinusoid at ''carrier frequency'' $\ (which is where you tune your AM radio). The Hilbert transform is almost exactly $y(t)\5.8, and the analytic signal is $z(t)\. Note that AM demodulation5.9 is now nothing more than the absolute value. I.e., $A(t) = \. Due to this simplicity, Hilbert transforms are sometimes used in makingamplitude envelope followers for narrowband signals (i.e., signals with all energy centered about a single ''carrier'' frequency). AM demodulation is one application of a narrowband envelope follower.

<< Previous page  TOC  INDEX  Next page >>