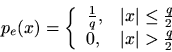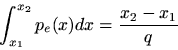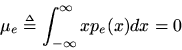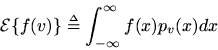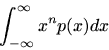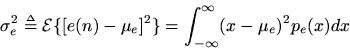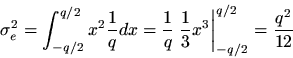Appendix A: Round-Off Error Variance

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Appendix A: Round-Off Error Variance

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Appendix A: Round-Off Error Variance

This section shows how to derive that the noise power of quantization error is $q^2/12$, where $q$ is the quantization step size.

Each round-off error in quantization noise $e(n)$ is modeled as a uniform random variable between $-q/2$ and $q/2$. It therefore has the probability density function (pdf)

\

Thus, the probability that a given roundoff error $e(n)$ lies in the interval $[x_1,x_2]$ is given by
\

assuming of course that $x_1$ and $x_2$ lie in the allowed range $[-q/2, q/2]$. We might loosely refer to $p_e(x)$ as a probability distribution, but technically it is a probability density function, and to obtain probabilities, we have to integrate over one or more intervals, as above. We use probability distributions for variables which take on discrete values (such as dice), and we use probabilitydensities for variables which take on continuous values (such as round-off errors).

The mean of a random variable is defined as

\

In our case, the mean is zero because we are assuming the use ofrounding (as opposed to truncation, etc.).

The mean of a signal $e(n)$ is the same thing as theexpected value of $e(n)$, which we write as ${\. In general, the expected value of any function $f(v)$ of a random variable $v$ is given by

\

Since the quantization-noise signal $e(n)$ is modeled as a series of independent, identically distributed (iid) random variables, we canestimate the mean by averaging the signal over time. Such an estimate is called a sample mean.

Probability distributions are often be characterized by theirmoments. The $n$th moment of the pdf $p(x)$ is defined as

\

Thus, the mean $\ is the first moment of the pdf. The second moment is simply the expected value of the random variable squared, i.e., ${\.

The variance of a random variable $e(n)$ is defined as thesecond central moment of the pdf:

\

''Central'' just means that the moment is evaluated after subtracting out the mean, that is, looking at $e(n)-\ instead of $e(n)$. In the case of round-off errors, the mean is zero, so subtracting out the mean has no effect. Plugging in the constant pdf for our random variable $e(n)$which we assume is uniformly distributed on $[-q/2, q/2]$, we obtain the variance
\

Note that the variance of $e(n)$ can be estimated by averaging $e^2(n)$over time, that is, by computing the mean square. Such an estimate is called the sample variance. For sampled physical processes, the sample variance is proportional to the average power in the signal. Finally, the square root of the sample variance (the rms level) is sometimes called the standard deviation of the signal, but this term is only precise when the random variable has a Gaussian pdf.

EE 278 is the starting course on statistical signal processing at Stanford if you are interested in this and related topics. A good text book on the subject is [13].

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy