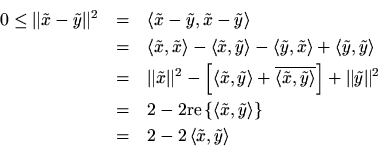NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Cauchy-Schwarz Inequality
The Cauchy-Schwarz Inequality (or ''Schwarz Inequality'') states that for all
and
, we have
with equality if and only iffor some scalar
.
We can quickly show this for real vectors
,
, as follows: If either
or
is zero, the inequality holds (as equality). Assuming both are nonzero, let's scale them to unit-length by defining the normalized vectors
,
, which are unit-length vectors lying on the ''unit ball'' in
(a hypersphere of radius
). We have
which implies
or, removing the normalization,
The same derivation holds ifyielding
The last two equations imply
The complex case can be shown by rotating the components ofbecomes equal to
.
