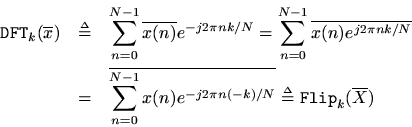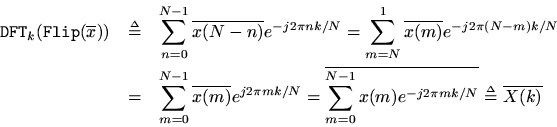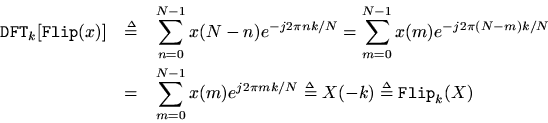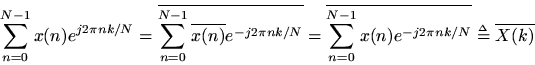Conjugation and Reversal

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Conjugation and Reversal

Theorem: For any ,

Proof:

Theorem: For any ,

Proof: Making the change of summation variable , we get

Theorem: For any ,

Proof:

Corollary: For any ,

Proof: Picking up the previous proof at the third formula, remembering that is real,

when is real.

Thus, conjugation in the frequency domain corresponds to reversal in the time domain. Another way to say it is that negating spectral phase flips the signal around backwards in time.

Corollary: For any ,

Proof: This follows from the previous two cases.

Definition: The property is called Hermitian symmetryor ''conjugate symmetry.'' If , it may be calledskew-Hermitian.

Another way to state the preceding corollary is

<< Previous page  TOC  INDEX  Next page >>