DB SPL

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

DB SPL

Sound Pressure Level (SPL) is defined using a reference which is approximately the intensity of 1000 Hz sinusoid that is just barely audible (0 ''phons''). In pressure units:

In intensity units:

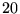
which corresponds to a root-mean-square (rms) pressure amplitude of Pa, or about Pa, as listed above. The wave impedanceof air plays the role of ''resistor'' in relating the pressure- and intensity-based references exactly analogous to the dBm case discussed above.

Since sound is created by a time-varying pressure, we compute sound levels in dB-SPL by using the average intensity (averaged over at least one period of the lowest frequency contained in the sound).

Table 4.1 gives a list list of common sound levels and their dBequivalents^4.5 [9]:

Table 4.1:Ballpark figures for the dB-SPL level of common sounds.

Sound dB-SPL Jet engine at 3m 140 Threshold of pain 130 Rock concert 120 Accelerating motorcycle at 5m 110 Pneumatic hammer at 2m 100 Noisy factory 90 Vacuum cleaner 80 Busy traffic 70 Quiet restaurant 50 Residential area at night 40 Empty movie house 30 Rustling of leaves 20 Human breathing (at 3m) 10 Threshold of hearing (good ears) 0

In my experience, the ''threshold of pain'' is most often defined as 120 dB.

The relationship between sound amplitude and actual loudness is complex [10]. Loudness is a perceptual dimension while sound amplitude is physical. Since loudness sensitivity is closer to logarithmic than linear in amplitude (especially at moderate to high loudnesses), we typically use decibels to represent sound amplitude, especially in spectral displays.

The sone amplitude scale is defined in terms of actual loudness perception experiments [10]. At 1kHz and above, loudness perception is approximately logarithmic above 50 dB SPL or so. Below that, it tends toward being more linear.

The phon amplitude scale is simply the dB scale at 1kHz [10, p. 111]. At other frequencies, the amplitude in phons is defined by following the equal-loudness curve over to 1 kHz and reading off the level there in dB SPL. In other words, all pure tones have the same loudness at the same phon level, and 1 kHz is used to set the reference in dB SPL. Just remember that one phon is one dB-SPL at 1 kHz. Looking at the Fletcher-Munson equal-loudness curves [10, p. 124], loudness in phons can be read off along the vertical line at 1 kHz.

Classically, the intensity level of a sound wave is its dB SPL level, measuring the peak time-domain pressure-wave amplitude relative to watts per centimeter squared (i.e., there is no consideration of the frequency domain here at all).

Another classical term still encountered is the sensation level of pure tones: The sensation level is the number of dB SPL above thehearing threshold at that frequency [10, p. 110].

For further information on ''doing it right,'' see, for example,
http://www.measure.demon.co.uk/Acoustics_Software/loudness.php.

<< Previous page  TOC  INDEX  Next page >>