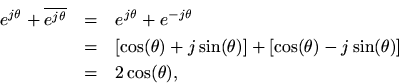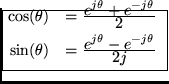NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Euler's Formula
Since
is the algebraic expression of
in terms of its rectangular coordinates, the corresponding expression in terms of its polar coordinates is
There is another, more powerful representation of
A proof of Euler's identity is given in the next chapter. Just note for the moment that forin terms of its polar coordinates. In order to define it, we must introduce Euler's Formula:
, we have
, as expected. Before, the only algebraic representation of a complex number we had was
, which fundamentally uses Cartesian (rectilinear) coordinates in the complex plane. Euler's identity gives us an alternative algebraic representation in terms of polar coordinates in the complex plane:
This representation often simplifies manipulations of complex numbers, especially when they are multiplied together. Simple rules of exponents can often be used in place of more difficult trigonometric identities. In the simplest case,
A corollary of Euler's identity is obtained by setting
to get
This has been called the ''most beautiful formula in mathematics'' due to the extremely simple form in which the fundamental constants, and
all appear.
For another example of manipulating the polar form of a complex number, let's again verify
, as we did above, but this time using polar form:
We can now add a fourth line to that set of examples:
Euler's identity can be used to derive formulas for sine and cosine in terms of
:
Similarly,, and we have