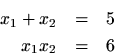NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Factoring a Polynomial with Real Roots

Remember ''factoring polynomials''? Consider the second-order polynomial

It is second-order because the highest power of is (only non-negative integer powers are allowed). The polynomial is also monic because its leading coefficient, the coefficient of , is . Since it is second order, there are at most two real roots (or zeros) of the polynomial. Suppose they are denoted and . Then we have and , and we can write

This is the factored form of the monic polynomial . (For a non-monic polynomial, we may simply divide all coefficients by the first to make it monic, and this doesn't affect the zeros.) Multiplying out the symbolic factored form gives

Comparing with the original polynomial, we find we must have

This is a system of two equations in two unknowns. Unfortunately, it is anonlinear system of two equations in two unknowns.^2.1Nevertheless, because it is so small, the equations are easily solved. In beginning algebra, we did them by hand. However, nowadays we can use a computer program such as Mathematica:

In[]:=
        Solve[{x1+x2==5, x1 x2 == 6}, {x1,x2}]
Out[]:
        {{x1 -> 2, x2 -> 3}, {x1 -> 3, x2 -> 2}}

Note that the two lists of substitutions points out that it doesn't matter which root is 2 and which is 3. In summary, the factored form of this simple example is

Note that polynomial factorization rewrites a monic th-order polynomial as the product of first-order monic polynomials, each of which contributes one zero (root) to the product. This factoring business is often used when working with digital filters.

<< Previous page  TOC  INDEX  Next page >>