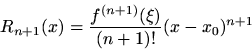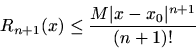Formal Statement of Taylor's Theorem

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Formal Statement of Taylor's Theorem

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>


Formal Statement of Taylor's Theorem

Let $f(x)$ be continuous on a real interval $I$ containing $x_0$ (and $x$), and let $f^{(n)}(x)$ exist at $x$ and $f^{(n+1)}(\ be continuous for all $\. Then we have the following Taylor series expansion:

\

where $R_{n+1}(x)$ is called the remainder term. There exists $\ between $x$ and $x_0$ such that
\

In particular, if $\ in $I$, then
\

which is normally small when $x$ is close to $x_0$.

When $x_0=0$, the Taylor series reduces to what is called a Maclaurin series.

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy