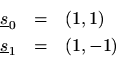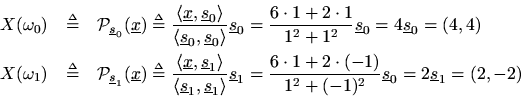NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

The Length 2 DFT

The length DFT is particularly simple, since the basissinusoids are real:

The DFT sinusoid is a sampled constant signal, while is a sampled sinusoid at half the sampling rate.

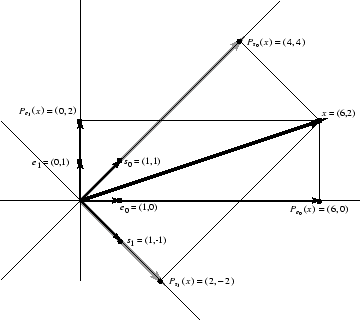
Figure 7.4 illustrates the graphical relationships for the length DFT of the signal .

Figure 7.4:Graphical interpretation of the length 2 DFT.

Analytically, we compute the DFT to be

Note the lines of orthogonal projection illustrated in the figure. The ''time domain'' basis consists of the vectors , and theorthogonal projections onto them are simply the coordinate projections and . The ''frequency domain'' basis vectors are , and they provide an orthogonal basis set which is rotated degrees relative to the time-domain basis vectors. Projecting orthogonally onto them gives and , respectively. The original signal can be expressed as the vector sum of its coordinate projections (a time-domain representation), or as the vector sum of its projections onto the DFT sinusoids (a frequency-domain representation). Computing the coefficients of projection is essentially ''taking the DFT'' and constructing as the vector sum of its projections onto the DFT sinusoids amounts to ''taking the inverse DFT.''

<< Previous page  TOC  INDEX  Next page >>