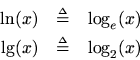NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Logarithms
A logarithm
is fundamentally an exponent
applied to a specific base
. That is,
. The term ''logarithm'' can be abbreviated as ''log''. The base
is chosen to be a positive real number, and we normally only take logs of positive real numbers
(although it is ok to say that the log of
is
). The inverse of a logarithm is called anantilogarithm or antilog.
For any positive number
, we have
for any valid base. This is just an identity arising from the definition of the logarithm, but it is sometimes useful in manipulating formulas.
When the base is not specified, it is normally assumed to be
, i.e.,
. This is the common logarithm.
Base 2 and base
logarithms have their own special notation:
(The use offor base
logarithms is common in computer science. In mathematics, it may denote a base
logarithm.) By far the most common bases are
,
, and
. Logs base
are called natural logarithms. They are ''natural'' in the sense that
while the derivatives of logarithms to other bases are not quite so simple:
(Prove this as an exercise.) The inverse of the natural logarithmis of course the exponential function
, and
is its own derivative.
In general, a logarithm
has an integer part and a fractional part. The integer part is called the characteristic of the logarithm, and the fractional part is called the mantissa. These terms were suggested by Henry Briggs in 1624. ''Mantissa'' is a Latin word meaning ''addition'' or ''make weight''--something added to make up the weight [6].
The following Matlab code illustrates splitting a natural logarithm into its characteristic and mantissa:
>> x = log(3) x = 1.0986 >> characteristic = floor(x) characteristic = 1 >> mantissa = x - characteristic mantissa = 0.0986
>> % Now do a negative-log example >> x = log(0.05) x = -2.9957 >> characteristic = floor(x) characteristic = -3 >> mantissa = x - characteristic mantissa = 0.0043Logarithms were used in the days before computers to performmultiplication of large numbers. Since
, one can look up the logs of
and
in tables of logarithms, add them together (which is easier than multiplying), and look up the antilog of the result to obtain the product
. Log tables are still used in modern computing environments to replace expensive multiplies with less-expensive table lookups and additions. This is a classic tradeoff between memory (for the log tables) and computation. Nowadays, large numbers are multiplied using FFT fast-convolution techniques.
Subsections