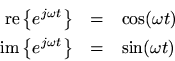Projection of Circular Motion

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Projection of Circular Motion

We have

Interpreting this in the complex plane tells us that sinusoidal motion is the projection of circular motion onto any straight line. Thus, the sinusoidal motion is the projection of the circular motion onto the (real-part) axis, while is the projection of onto the (imaginary-part) axis.

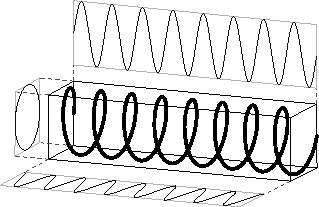
Figure 5.7 shows a plot of a complex sinusoid versus time, along with its projections onto coordinate planes. This is a 3D plot showing the-plane versus time. The axes are the real part, imaginary part, and time. (Or we could have used magnitude and phase versus time.)

Figure 5.7:A complex sinusoid and its projections.

Note that the left projection (onto the plane) is a circle, the lower projection (real-part vs. time) is a cosine, and the upper projection (imaginary-part vs. time) is a sine. A point traversing the plot projects to uniform circular motion in the plane, and sinusoidal motion on the two other planes.

<< Previous page  TOC  INDEX  Next page >>