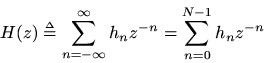Transfer Function

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Transfer Function

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Transfer Function

The transfer function associated with any filter is defined as the $z$ transform of its impulse response. For the FIR filter we have

\

Thus, the transfer function of every length $N+1$ causal FIR filter is an $N$th-order polynomial in $z$.

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy