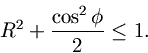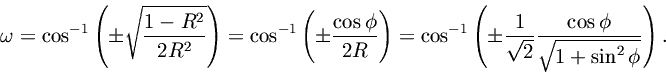06. Minimum Phase (MP) polynomials in Z

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Minimum Phase (MP) polynomials in

All properties of MP polynomials apply without modification to marginallystable allpole transfer functions (cf. Thm. (1)).

Every first-order MP polynomial is positive real.

Every first-order MP polynomial $b(z)=1+b_1 z^{-1}$ is such that $$ \$ is positive real.

A PR second-order MP polynomial with complex-conjugate zeros,

$$\$ $$\$ $$\$ (38)

$$\$ $$\$ (39)

satisfies

If $$2R^2+\$ , then $$\$ has a double zero at

All polynomials of the form

are positive real. (These have zeros uniformly distributed on a circle of radius.)