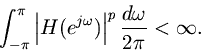14. Vector Space Concepts

GUIDE: Elementary Digital Filter Theory - Julius O. Smith III. Vector Space Concepts

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Vector Space Concepts

Definition. A set $X$ of objects is called a metric spaceif with any two points $p$ and $q$ of $X$ there is associated a real number$d(p,q)$, called the distance from $p$ to $q$, such that (a) $d(p,q)>0$ if $p\; $d(p,p)=0$, (b) $d(p,q)=d(q,p)$, (c) $d(p,q)\, for any $r\ [Rudin 1964].

Definition. A linear space is a set of ``vectors'' $X$ together with a field of ``scalars'' ${\ with an addition operation $+:X\, and a multiplication opration $\taking ${\, with the following properties: If $x$, $y$, and $z$ are in $X$, and $\ are in ${\, then

  1. $x+y=y+x$.
  2. $x+(y+z)=(x+y)+z$.
  3. There exists $\ in $X$ such that $0\for all $x$ in $X$.
  4. $\.
  5. $(\.
  6. $1\.
  7. $\.
The element $\ is written as $0$ thus coinciding with the notation for the real number zero. A linear space is sometimes be called a linear vector space, or a vector space.

Definition. A normed linear space is a linear space $X$ on which there is defined a real-valued function of $x\ called a norm, denoted $ \, satisfying the following three properties:

  1. $\, and $\.
  2. $\, $c$ a scalar.
  3. $\.
The functional $ \ serves as a distance function on $X$, so a normed linear space is also a metric space.

Note that when $X$ is the space of continuous complex functions on the unit circle in the complex plane, the norm of a function is not changed when multiplied by a function of modulus $1$ on the unit circle. In signal processing terms, the norm is insensitive to multiplication by a unity-gain allpass filter (also known as a Blaschke product).

Definition. A pseudo-norm is a real-valued function of $x\ satisfying the following three properties:

  1. $\, and $x=0\.
  2. $\, $c$ a scalar.
  3. $\.
A pseudo-norm differs from a norm in that the pseudo-norm can be zero for nonzero vectors (functions).

Definition. A Banach Space is a complete normed linear space, that is, a normed linear space in which every Cauchy sequence2*A sequence $H_n(e^{j\ is said to be a Cauchy sequence if for each $\ there is an $N$ such that $ \ for all $n$ and $m$ larger than $N$. converges to an element of the space.

Definition. A function $H(e^{j\ is said to belong to the space $Lp$ if

\

Definition. A function $H(e^{j\ is said to belong to the space $H^p$ if it is in $Lp$ and if its analytic continuation $H(z)$ is analytic for$\. $H(z)$ is said to be in $H^{-p}$ if $H(z^{-1})\.

Theorem. (Riesz-Fischer) The $Lp$ spaces are complete.Proof. See Royden [Royden 1968], p. 117.

Definition. A Hilbert space is a Banach space with a symmetric bilinearinner product $<x,y>$ defined such that the inner product of a vector with itself is the square of its norm $<x,x>= \.

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy