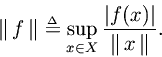16. Concavity (Convexity)

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Concavity (Convexity)

Definition. A set is said to be concave if for every vector and in , is in for all . In other words, all points on the line between two points of lie in .

Definition. A functional is a mapping from a vector space to the real numbers .

Thus, for example, every norm is a functional.

Definition. A linear functional is a functional such that for each and in the linear space , and for all scalars and , we have .

Definition. The norm of a linear functional is defined on the normed linear space by

Definition. A functional defined on a concave subset of a vector space is said to be concave on if for every vector and in ,

A concave functional has the property that its values along a line segment lie below or on the line between its values at the end points. The functional is strictly concave on if strict inequality holds above for . Finally, isuniformly concave on if there exists such that for all ,

We have

Definition. A local minimizer of a real-valued function is any such that in some neighborhood of .

Definition. A global minimizer of a real-valued function on a set is any such that for all .

Definition. A cluster point of a sequence is any point such that every neighborhood of contains at least one .

Definition. The concave hull of a set in a metric space is the smallest concave set containing .

<< Previous page  TOC  INDEX  Next page >>