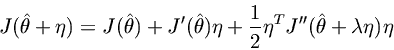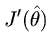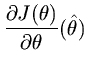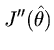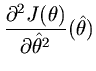NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Taylor's Theorem
Theorem. (Taylor) Every functional
in
has the representation
for somebetween
and
, where
is the
gradientvector evaluated at
, and
is the
Hessian matrix of
at
, i.e.,
(52) (53)
Proof. See Goldstein [Goldstein 1967] p. 119. The Taylor infinite series is treated in Williamson and Crowell [Williamson et al. 1972]. The present form is typically more useful for computing bounds on the error incurred by neglecting higher order terms in the Taylor expansion.