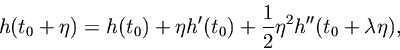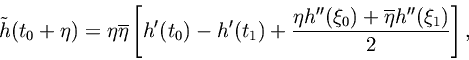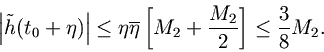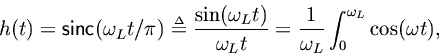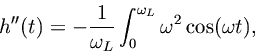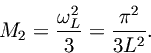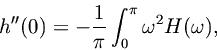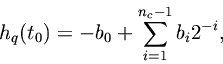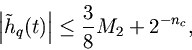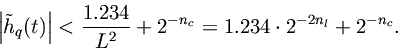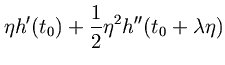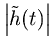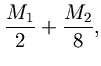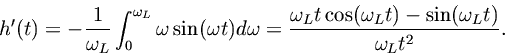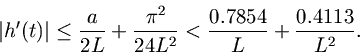10. Choice of Table Size

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "The Digital Audio Resampling Home Page", by Julius O. Smith III, Copyright © 2016-05-17 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC Next page >>

Choice of Table Size

It is desirable that the stored filter impulse response be sampled sufficiently densely so that interpolating linearly between samples does not introduce error greater than the quantization error. We will show that this condition is satisfied whenever the filter table contains at least $L=2^{1+{n_c}/2}$ entries per zero-crossing, where ${n_c}$ is the number of bits allocated to each table entry.

Linear Interpolation Error Bound.

Let denote the lowpass filter impulse response, and assume it is twice continuously differentiable for all . By Taylor's theorem[Goldstein 1967, p. 119], we have

for some $$\$ , where $$h^\$ denotes the time derivative of evaluated at , and $$h^{\$ is the second derivative at.
The linear interpolation error is defined as

where $$t=t_0+\$ , $$t_0=\$ , $$\$ , and $$\$ is the interpolated value given by

where $$\$ and $$t_1\$ . Thus and are successive time instants for which samples of are available, and $$\$ is the linear interpolation factor. (We ignore errors in the linear interpolation itself at this point.)
Expressing as

applying Eq. (2.6.1) to both terms on the right-hand side, and subtracting Eq. (2.6.1) gives

where both $$\$ and $$\$ are in . Defining

and noting that $$h^\$ for some $$\$ which implies

we obtain the upper bound

Application to the Ideal Lowpass Filter.

For the ideal lowpass filter, we have

where $$\$ , and $L=2^{{n_l}}$ is the number of table entries per zero-crossing. Note that the rightmost form in Eq. (2.6.1) is simply the inverse Fourier transform of the ideal lowpass-filter frequency response. Twice differentiating with respect to , we obtain

from which it follows that the maximum magnitude is

Note that this bound is attained at . Substituting Eq. (2.6.1) into Eq. (2.6.1), we obtain the error bound

Thus for the ideal lowpass filter $$h(t)=\$ , the pointwise error in the interpolated lookup of is bounded by . This means that ${n_l}$ must be about half the coefficient word-length ${n_c}$ used for the filter coefficients. For example, if is quantized to bits, must be of the order of $2^{16/2}=256$ . In contrast, we will show that without linear interpolation, ${n_l}$ must increase proportional to ${n_c}$ for ${n_c}$ -bit samples of . In the -bit case, this gives $$L\$ . The use of linear interpolation of the filter coefficients reduces the memory requirements considerably.
The error bounds obtained for the ideal lowpass filter are typically accurate also for lowpass filters used in practice. This is because the error bound is a function of , the maximum curvature of the impulse response , and most lowpass designs will have a value of very close to that of the ideal case. The maximum curvature is determined primarily by the bandwidth of the filter since, generalizing equations Eq. (2.6.1) and Eq. (2.6.1),

which is just the second moment of the lowpass-filter frequency response $$H(\$ (which is real for symmetric FIR filters obtained by symmetrically windowing the ideal sinc function [Rabiner and Gold 1975]). A lowpass-filter design will move the cut-off frequency slightly below that of the ideal lowpass filter in order to provide a ``transition band'' which allows the filter response to give sufficient rejection at the ideal cut-off frequency which is where aliasing begins. Therefore, in a well designed practical lowpass filter, the error bound should be lower than in the ideal case.

Relation of Interpolation Error to Quantization Error.

If $$h(t)\$ is approximated by which is represented in two's complement fixed-pointarithmetic, then

where $$b_i\$ is the th bit, and the worst-case rounding error is

Letting $$h_q(t_i)=h(t_i)+\$ , where $$\$ , the interpolated look-up becomes

Thus the error in the interpolated lookup between quantized filter coefficients is bounded by

which, in the case of $$h(t)=\$ , can be written

If $L=2^{1+{n_c}/2}$ , then $$\$ , and the interpolation error is less than the quantization error by more than a factor of .

Error in the Absence of Interpolation.

For comparison purposes, we derive the error incurred when no interpolation of the filter table is performed. In this case, assuming rounding to the nearest table entry, we have

$$\$ $$\$ $$\$ (5)

$$\$ $$\$ $$\$ (6)

$$\$ $$\$ $$\$ (7)

$$\$ $$\$ (8)

$$\$ $$\$ $$\$ (9)

where $$M_1 \$ . For the ideal lowpass, we have

Note that $$h^\$ and $$\$ . Thus where $$1\$ . The no-interpolation error bound is then