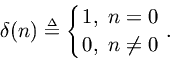10. Difference Equation

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Difference Equation

Definition. The difference equation for a general linear time-invariant (LTI)digital filter is given by

			(42)
			(43)

where is the input signal, is the output signal, and the constants , , , are called difference equation coefficients, or more simply, filter coefficients. When the and coefficients are real numbers, then the filter is said to be real.

Definition. Equation Eq. (43) represents only causal LTI filters. A filter is said to be causal when the output does not depend on any ``future'' inputs. (In more colorful terms, a filter is causal if it does not ``laugh'' before it is ``tickled.'')

Definition. The maximum time span, in samples, used in creating each output sample is called the order of the filter. In Eq. (43), the order is the larger of and . Since and in Eq. (43) are assumed finite, Eq. (43) represents the class of finite order causal LTI filters.

In addition to difference equation coefficients, any LTI filter may be represented in the time domain by its response to a specific signal called the impulse.

Definition. The impulse is denoted as and is defined by

Definition. The impulse response of a filter is the response of the filter to and is most often denoted .

Definition. A filter is said to be stable if the impulse response approaches zero as goes to infinity.

<< Previous page  TOC  INDEX  Next page >>