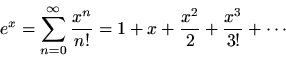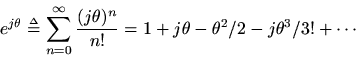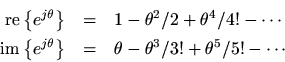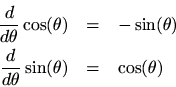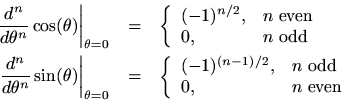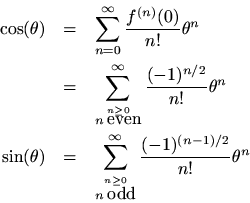NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Back to e^(j theta)
We've now defined
for any positive real number
and any complex number
. Setting
and
gives us the special case we need for Euler's identity. Since
is its own derivative, the Taylor series expansion for for
is the simplest series there could be:
The simplicity comes about becausefor all
and because we chose to expand about the point
. We of course define
Note that all even order terms are real while all odd order terms are imaginary. Separating out the real and imaginary parts gives
Comparing the Maclaurin expansion for
with that of
and
proves Euler's identity. Recall that
so that
Plugging into the general Maclaurin series gives
Separating the Maclaurin expansion for
thus proving Euler's identity.
