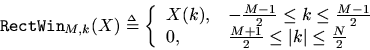Bandlimited Interpolation in Time

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Bandlimited Interpolation in Time

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Bandlimited Interpolation in Time

The dual of the Zero-Padding Theorem states formally that zero padding in the frequency domain corresponds to ideal bandlimited interpolation in the time domain. However, we have not precisely defined ideal bandlimited interpolation in the time domain. Therefore, we'll let the dual of the Zero-Padding Theorem provide its definition:



Definition: For all $x\ and any integer $L\,

\

where the zero-padding is of the frequency-domain type, as described earlier and illustrated in Fig. 8.5.

It is instructive to interpret the Interpolation Theorem in terms of theStretch Theorem $\. To do this, it is convenient to define a ''zero-centered rectangular window'' operator:



Definition: For any $X\ and any odd integer $M<N$ we define the length $M$ even rectangular windowing operation by

\

Thus, the ''zero-phase rectangular window,'' when applied to a spectrum$X$, sets the spectrum to zero everywhere outside a zero-centered interval of $M$ samples. Note that $\ is the ideal lowpassfiltering operation in the frequency domain, where the lowpass ''cut-off frequency'' in radians per sample is $\. With this we can efficiently show the basic theorem of ideal bandlimited interpolation:



Theorem: For $x\,

\

In other words, ideal bandlimited interpolation of $x$ by the factor $L$may be carried out by first stretching $x$ by the factor $L$ (i.e., inserting $L-1$ zeros between adjacent samples of $x$), taking the DFT, applying the ideal lowpass filter, and performing the inverse DFT.

Proof: First, recall that $\, that is, stretching a signal by the factor $L$ gives a new signal $y=\ which has a spectral grid $L$ times the density of $X$, and the spectrum $Y$ contains$L$ copies of $X$ repeated around the unit circle. The ''baseband copy'' of $X$ can be defined as the width $N$ sequence centered about frequency zero. Therefore, if we can use an ''ideal filter'' to ''pass'' the baseband spectral copy and zero out all others, we can convert $\ to $\. I.e.,

\

where the last step is by definition of time-domain ideal bandlimited interpolation.

Note that the definition of ideal bandlimited time-domain interpolation in this section is only really ideal for signals which are periodic in$N$ samples. To see this, consider that the rectangular windowing operation in the frequency domain corresponds to cyclic convolutionin the time domain,8.8 and cyclic convolution is only the same as acyclic convolution when one of the signals is truly periodic in $N$ samples. Since all spectra $X\ are truly periodic in $N$ samples, there is no problem with the definition of ideal spectral interpolation used in connection with the Zero-Padding Theorem. However, for a more practical definition of ideal time-domain interpolation, we should use instead the dual of the Zero-Padding Theorem for the DTFT case. Nevertheless, for signals which areexactly periodic in $N$ samples (a rare situation), the present definition is ideal.

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy