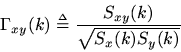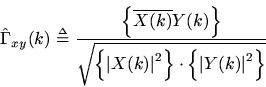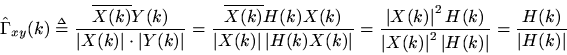NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Coherence
A function related to cross-correlation is the coherence function
, defined in terms of power spectral densities and the cross-spectral density by
In practice, these quantities can be estimated by averaging,
and
over successive signal blocks. Let
denote time averaging. Then an estimate of the coherence, the sample coherence function
, may be defined by
The magnitude-squared coherence
is a real function between
and
which gives a measure of correlation between
and
at each frequency (DFT bin number
). For example, imagine that
is produced from
via an LTI filtering operation:
Then the coherence function is
and the magnitude-squared coherence function is simply
On the other hand, ifand
are uncorrelated noise processes, the coherence converges to zero.
A common use for the coherence function is in the validation of input/output data collected in an acoustics experiment for purposes of system identification. For example,
might be a known signal which is input to an unknown system, such as a reverberant room, say, and
is the recorded response of the room. Ideally, the coherence should be
at all frequencies. However, if the microphone is situated at a nullin the room response for some frequency, it may record mostly noise at that frequency. This will be indicated in the measured coherence by a significant dip below
.