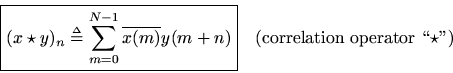Correlation

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Correlation

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Correlation



Definition: The correlation operator for two signals $x$ and $y$ in ${\is defined as

\

We may interpret the correlation operator as

\

which is the coefficient of projection onto $x$ of $y$ advanced by$n$ samples (shifted circularly to the left by $n$ samples). The time shift $n$ is called the correlation lag, and $\ is called a lagged product. Applications of correlation are discussed in §8.8.

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy