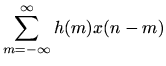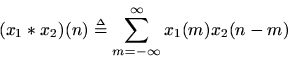Convolution Representation

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Convolution Representation

Note that the output of the th delay element in Fig. B.1 is, , where is the input signalamplitude at time . The output signal is therefore

			(B.1)
			(B.2)
			(B.3)
			(B.4)

where we have used the convolution operator '''', defined in general for any two signals , as

An FIR filter thus operates by convolving the input signal with the filter's impulse response .

<< Previous page  TOC  INDEX  Next page >>