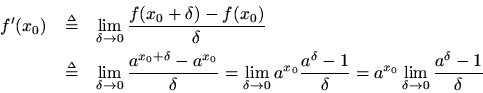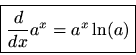Derivatives of f(x)=a^x

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Derivatives of f(x)=a^x

Let's apply the definition of differentiation and see what happens:

Since the limit of as is less than 1 for and greater than for (as one can show via direct calculations), and since is a continuous function of, it follows that there exists a positive real number we'll call such that for we get

For , we thus have .

So far we have proved that the derivative of is . What about for other values of ? The trick is to write it as

and use the chain rule. Formally, the chain rule tells us how do differentiate a function of a function as follows:

In this case, so that , and which is its own derivative. The end result is then , i.e.,

<< Previous page  TOC  INDEX  Next page >>