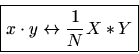NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Dual of the Convolution Theorem
The Dual8.7 of the Convolution Theorem says thatmultiplication in the time domain is convolution in thefrequency domain:
Theorem:
Proof: The steps are the same as in the Convolution Theorem.
This theorem also bears on the use of FFT windows. It says that windowing in the time domain corresponds to smoothing in the frequency domain. That is, the spectrum of
is simply
filtered by
, or,
. This smoothing reduces sidelobesassociated with the rectangular window (which is the window one gets implicitly when no window is explicitly used). FFT windows are covered inMusic 420.