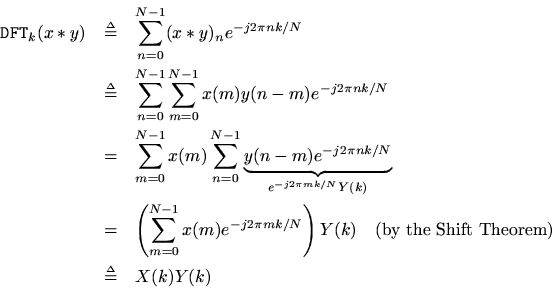NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Convolution Theorem
Theorem: For any,
Proof:
This is perhaps the most important single Fourier theorem of all. It is the basis of a large number of applications of the FFT. Since the FFT provides a fast Fourier transform, it also provides fast convolution, thanks to the convolution theorem. It turns out that using the FFT to perform convolution is really more efficient in practice only for reasonably long convolutions, such as. For much longer convolutions, the savings become enormous compared with ''direct'' convolution. This happens because direct convolution requires on the order of
operations (multiplications and additions), while FFT-based convolution requires on the order of
operations.
The following simple Matlab example illustrates how much faster convolution can be performed using the FFT:
>> N = 1024; % FFT much faster at this length >> t = 0:N-1; % [0,1,2,...,N-1] >> h = exp(-t); % filter impulse reponse = sampled exponential >> H = fft(h); % filter frequency response >> x = ones(1,N); % input = dc (any example will do) >> t0 = clock; y = conv(x,h); t1 = etime(clock,t0); % Direct >> t0 = clock; y = ifft(fft(x) .* H); t2 = etime(clock,t0); % FFT >> sprintf(['Elapsed time for direct convolution = %f sec\n',... 'Elapsed time for FFT convolution = %f sec\n',... 'Ratio = %f (Direct/FFT)'],t1,t2,t1/t2)
ans =
Elapsed time for direct convolution = 8.542129 sec Elapsed time for FFT convolution = 0.075038 sec Ratio = 113.837376 (Direct/FFT)