NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
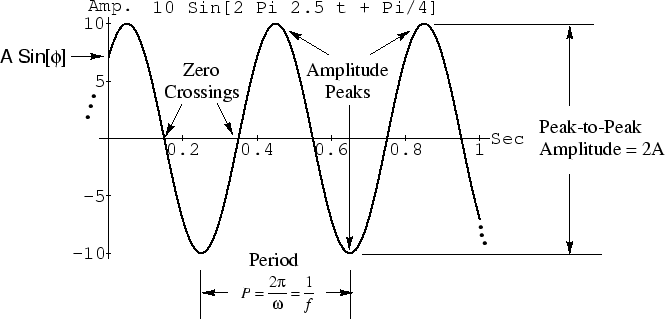
Example Sinusoids
Figure 5.1 plots the sinusoid
, for
,
,
, and
. Study the plot to make sure you understand the effect of changing each parameter (amplitude, frequency, phase), and also note the definitions of ''peak-to-peak amplitude'' and ''zero crossings.''
The Mathematica code for generating this figure is listed in §5.4.
A ''tuning fork'' vibrates approximately sinusoidally. An ''A-440'' tuning fork oscillates at
cycles per second. As a result, a tone recorded from an ideal A-440 tuning fork is a sinusoid at
Hz. The amplitude
determines how loud it is and depends on how hard we strike the tuning fork. The phase
is set by exactly when we strike the tuning fork (and on our choice of when time 0 is). If we record an A-440 tuning fork on an analog tape recorder, the electrical signal recorded on tape is of the form
As another example, the sinusoid at amplitude
and phase
(90 degrees) is simply
Thus,is a sinusoid at phase 90-degrees, while
is a sinusoid at zero phase. Note, however, that we could just as well have defined
to be the zero-phase sinusoid rather than
. It really doesn't matter, except to be consistent in any given usage. The concept of a ''sinusoidal signal'' is simply that it is equal to a sine or cosine function at some amplitude, frequency, and phase. It does not matter whether we choose
or
in the ''official'' definition of a sinusoid. You may encounter both definitions. Using
is nice since ''sinusoid'' in a sense generalizes
. However, using
is nicer when defining a sinusoid to be the real part of a complex sinusoid (which we'll talk about later).