NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW
VERSION: "Mathematics of the Discrete
Fourier Transform (DFT), with Audio Applications --- Second
Edition", by Julius
O. Smith III, W3K
Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright ©
2017-09-28 by Julius O. Smith III -
Center for Computer Research
in Music and Acoustics (CCRMA), Stanford University
<<
Previous page TOC INDEX Next
page >>
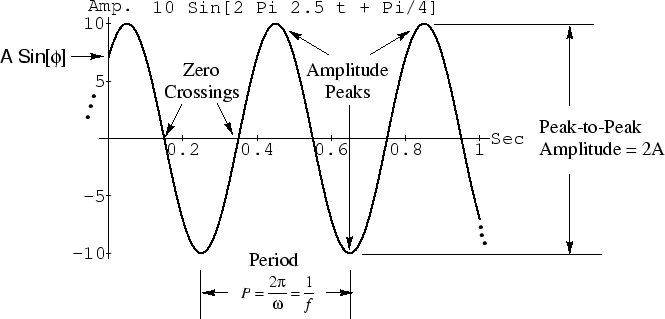
Figure 5.1
plots the sinusoid
, for 
, 
,
, and
. Study the plot to make sure you understand the effect of
changing each parameter (amplitude,
frequency,
phase), and also note the definitions of ''peak-to-peak amplitude''
and ''zero crossings.''
Figure 5.1:An example
sinusoid.
|
|
The Mathematica
code for generating this figure is listed in §5.4.
A ''tuning fork'' vibrates approximately sinusoidally. An
''A-440'' tuning fork oscillates at 
cycles
per second. As a result, a tone recorded from an ideal A-440 tuning
fork is a sinusoid at 
Hz. The amplitude
determines how loud it is and depends on how hard we strike the
tuning fork. The phase 
is set by exactly when we strike the tuning fork
(and on our choice of when time 0 is). If we record an A-440 tuning
fork on an analog tape recorder, the electrical signal recorded on
tape is of the form
As another example, the sinusoid at amplitude 
and phase
(90
degrees) is simply
Thus, 
is a sinusoid at phase 90-degrees, while 
is a sinusoid at zero phase. Note, however, that we could
just as well have defined to be the zero-phase sinusoid rather than . It really doesn't matter, except to be consistent in any
given usage. The concept of a ''sinusoidal signal'' is simply that
it is equal to a sine or cosine function at some amplitude,
frequency, and phase. It does not matter whether we choose
or
in
the ''official'' definition of a sinusoid. You may encounter both
definitions. Using is nice since ''sinusoid'' in a sense generalizes
.
However, using is nicer when defining a sinusoid to be the real part of a
complex sinusoid (which we'll talk about later).
<<
Previous page TOC INDEX Next
page >>
