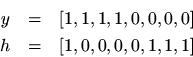NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW
VERSION: "Mathematics of the Discrete
Fourier Transform (DFT), with Audio Applications --- Second
Edition", by Julius
O. Smith III, W3K
Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright ©
2017-09-28 by Julius O. Smith III -
Center for Computer Research
in Music and Acoustics (CCRMA), Stanford University
<<
Previous page TOC INDEX Next
page >>
Note that the cyclic convolution
operation can be expressed in terms of previously defined operators
as
where 
and 
. It is instructive to interpret the last expression above
graphically.
Figure 8.3:Illustration of
convolution of ![$y=[1,1,1,1,0,0,0,0]$](https://technick.net/img/guide_dft/img28.png)
and its ''matched
filter'' h=[1,0,0,0,0,1,1,1] (
).
|
|
Figure 8.3
illustrates convolution of
For example, 
could
be a ''rectangularly windowed signal, zero-padded by a factor of
2,'' where the signal happened to be dc (all 
s). For
the convolution, we need
which is the same as . When 
, we say that 
ismatched filter for .8.3 In this case, is
matched to look for a ''dc component,'' and also zero-padded by a
factor of 
. The
zero-paddingserves
to simulate acyclic convolution using circular convolution. The
figure illustrates the computation of the convolution of
and
:
Note that a large peak is obtained in the convolution output at
time 
. This
large peak (the largest possible if all signals are limited
to![$[-1,1]$](https://technick.net/img/guide_dft/img1103.png)
in
magnitude), indicates the matched filter has ''found'' the dc
signal starting at time . This peak would persist even if varioussinusoids
at other frequencies and/or noise were
added in.
<<
Previous page TOC INDEX Next
page >>
