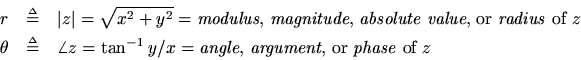NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
More Notation and Terminology
It's already been mentioned that the rectilinear coordinates of a complex number
in the complex plane are called the real part andimaginary part, respectively.
We also have special notation and various names for the radius and angle of a complex number
expressed in polar coordinates
:
The complex conjugate of
and is defined by
where, of course,. Sometimes you'll see the notation
in place of
In general, you can always obtain the complex conjugate of any expression by simply replacing
with
. In the complex plane, this is a vertical flip about the real axis; in other words, complex conjugation replaces each point in the complex plane by its mirror image on the other side of the
axis.
