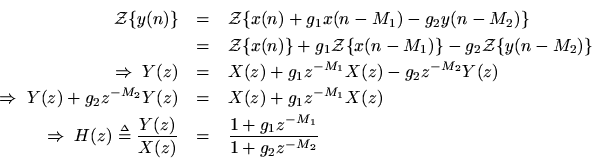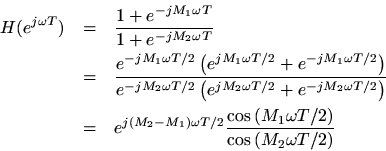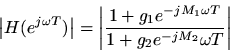Motivating Example and Overview

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Motivating Example and Overview

Suppose you look up the documentation for a ''comb filter'' in a software package you are using, and you find it described as follows:
out(n) = input(n) + feedforward * input(n-delay1) - feedback * out(n-delay2)
Does this tell you everything you need to know? Well, it does tell you exactly what is implemented, but to really understand it, you need to see its frequency response. Moreover, if delay2corresponds to more than a a few milliseconds, you probably want to see its impulse response as well. The purpose of this appendix is to describe how to do this analysis.
To analyze our example, let's first write it in a more ''mathematical'' form:

The transfer function is derived by taking the transform of both side of this equation and solving for the transfer function, defined as :

The principles of this derivation are as follows

The transform $${\$ is a linear operator which implies

$$x(n-M)\$ . That is, the transform of a signal delayed by samples, $$x(n-M),\$ , has the transform $z^{-M}X(z)$ . This is the shift theorem for transforms, which can be immediately derived from the definition of the transform, as we do below.

Given the transfer function , the frequency response is obtained by setting $$z=e^{j\$ , where is the sampling interval in seconds, and $$\$ is radian frequency which ranges from $$-\$ (minus half the sampling rate in radians per second) to $$\$ (plus half the sampling rate).

In the special case , we obtain

This special case gives insight into the behavior of the filter as its coefficients and get approach 1. When , the filter degenerates to which corresponds to ; in this case, the delayed input and output signals cancel each other out.
Since the frequency response is a complex-valued function, it has amagnitude and phase angle. The magnitude of the frequency response is called the amplitude response, and gives the filter gain at each frequency $$\$ . In this example, the amplitude response is

which, for , reduces to

$$\$ FIXME: Give Matlab code and plot of amplitude response here $$\$

The phase of the frequency response is called the phase response. Like the phase of any complex number, it is given by the arctangent of the imaginary part of $$H(e^{j\$ divided by its real part, and it contains information about the delay of the filter at each frequency. The phase response is a good measure of filter delay when those delays are short (less than a few milliseconds, say). For longer delays, it is usually best to study the filterimpulse response, which can be defined as the inverse- transform of the filter transfer function (or the inverse Fourier transform of the frequency response).

$$\$ FIXME: Give Matlab code and plot of phase response and impulse response $$\$

This section has provided an overview of filter analysis in the frequency domain. We see that a complete understanding of this analysis requires understanding ofcomplex numbers and the elements of the transform. A tutorial introduction to these topics is provided in Music 320 Background Reader. Here we will assume that background and focus on practical digital filterstructures and their frequency-domain analysis.

<< Previous page TOC INDEX Next page >>

Motivating Example and Overview

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Motivating Example and Overview

Motivating Example and Overview