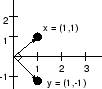Orthogonality

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Orthogonality

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Orthogonality

The vectors (signals) $x$ and $y$ are said to be orthogonal if $\, denoted $x\. That is to say

\

Note that if $x$ and $y$ are real and orthogonal, the cosine of the angle between them is zero. In plane geometry ($N=2$), the angle between twoperpendicular lines is $\, and $\, as expected. More generally, orthogonality corresponds to the fact that two vectors in$N$-space intersect at a right angle and are thus perpendiculargeometrically.

Example ($N=2$):

Let $x=[1,1]$ and $y=[1,-1]$, as shown in Fig. 6.8.

Figure 6.8:Example of two orthogonal vectors for $N=2$.
\

The inner product is $\. This shows that the vectors are orthogonal. As marked in the figure, the lines intersect at a right angle and are therefore perpendicular.

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy