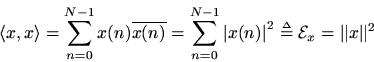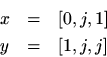NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

The Inner Product

The inner product (or ''dot product'') is an operation on two vectors which produces a scalar. Adding an inner product to a Banach space produces a Hilbert space (or ''inner product space''). There are many examples of Hilbert spaces, but we will only need for this course (complex length vectors with complex scalars).

The inner product between two (complex) -vectors and is defined by

The complex conjugation of the second vector is done in order that a norm will be induced by the inner product:

As a result, the inner product is conjugate symmetric:

Note that the inner product takes to . That is, two length complex vectors are mapped to a complex scalar.

Example:For we have, in general,

Let

Then

---

Subsections

• Linearity of the Inner Product
• Norm Induced by the Inner Product
• Cauchy-Schwarz Inequality
• Triangle Inequality
• Triangle Difference Inequality
• Vector Cosine
• Orthogonality
• The Pythagorean Theorem in N-Space
• Projection

<< Previous page  TOC  INDEX  Next page >>