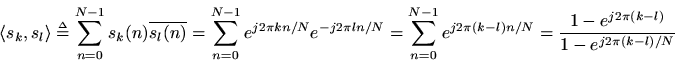NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Orthogonality of the DFT Sinusoids
We now show mathematically that the DFT sinusoids are exactly orthogonal. Let
denote theth complex DFT sinusoid. Then
where the last step made use of the closed-form expression for the sum of ageometric series. If, the denominator is nonzero while the numerator is zero. This proves
While we only looked at unit amplitude, zero phase complex sinusoids, as used by the DFT, it is readily verified that the (nonzero) amplitude and phase have no effect on orthogonality.