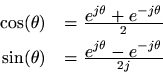NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Positive and Negative Frequencies
Earlier, we used Euler's Identity to show
Setting, we see that both sine and cosine (and hence all real sinusoids) consist of a sum of equal and opposite circular motion. Phrased differently, every real sinusoid consists of an equal contribution of positive and negative frequency components. This is true of all real signals. When we get to spectrum analysis, we will find that every real signal contains equal amounts of positive and negative frequencies, i.e., if
denotes the spectrum of the real signal
, we will always have
.
Note that, mathematically, the complex sinusoid
is really simpler and more basic than the real sinusoid
because
consists of one frequency
while
really consists of two frequencies
and
. We may think of a real sinusoid as being the sum of a positive-frequency and a negative-frequency complex sinusoid, so in that sense real sinusoids are ''twice as complicated'' as complex sinusoids. Complex sinusoids are also nicer because they have a constant modulus. ''Amplitude envelope detectors'' for complex sinusoids are trivial: just compute the square root of the sum of the squares of the real and imaginary parts to obtain the instantaneous peak amplitude at any time. Frequency demodulators are similarly trivial: just differentiate the phase of the complex sinusoid to obtain its instantaneous frequency. It should therefore come as no surprise that signal processing engineers often prefer to convert real sinusoids into complex sinusoids before processing them further.