NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Shift Operator
Definition: The shift operator is defined by
anddenotes the entire shifted signal. Note that since indexing is modulo
, the shift is circular. However, we normally use it to represent time delay by
samples. We often use the shift operator in conjunction with zero padding(appending zeros to the signal
) in order to avoid the ''wrap-around'' associated with a circular shift.
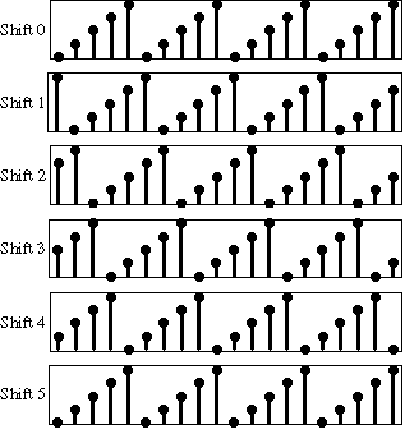
Figure 8.2:Successive one-sample shifts of a sampled periodic sawtooth waveform having first period .
Figure 8.2 illustrates successive one-sample delays of a periodic signal having first period given by
.
Example:(an impulse delayed one sample).
Example:(a circular shift example).
Example:(another circular shift example).