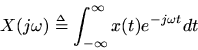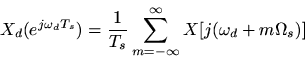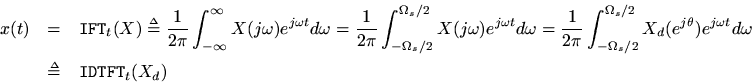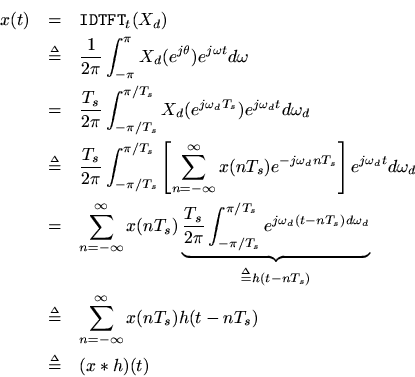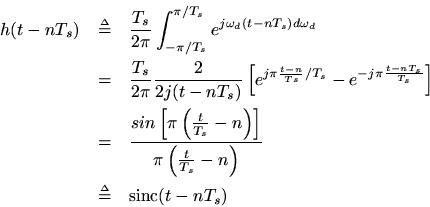Shannon's Sampling Theorem

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Shannon's Sampling Theorem

Theorem. Let denote any continuous-time signal having a continuous Fourier transform

Let

denote the samples of at uniform intervals of seconds. Then can be exactly reconstructed from its samples if and only if $$X(j\$ for all $$\$ .^A.1
Proof. From the Continuous-Time Aliasing Theorem of §A.2, we have that the discrete-time spectrum $$X_d(e^{j\$ can be written in terms of the continuous-time spectrum $$X(j\$ as

where $$\$ is the ''digital frequency'' variable. If $$X(j\$ for all $$\$ , then the above infinite sum reduces to one term, the term, and we have

At this point, we can see that the spectrum of the sampled signal coincides with the spectrum of the continuous-time signal. In other words, the DTFT of is equal to the FT of between plus and minus half the sampling rate, and the FT is zero outside that range. This makes it clear that spectral information is preserved, so it should now be possible to go from the samples back to the continuous waveform without error.
To reconstruct from its samples , we may simply take the inverse Fourier transform of the zero-extended DTFT, i.e.,

By expanding $$X_d(e^{j\$ as the DTFT of the samples , the formula for reconstructing as a superposition of sinc functionsweighted by the samples, depicted in Fig. A.1, is obtained:

where we defined

I.e.,

The ''sinc function'' is defined with $$\$ in its argument so that it has zero crossings on the integers, and its peak magnitude is 1. Figure A.2illustrates the appearance of the sinc function.
We have shown that when is band-limited to less than half the sampling rate, the IFT of the zero-extended DTFT of its samples gives back the original continuous-time signal .

Conversely, if can be reconstructed from its samples $$x_d(n) \$ , it must be true that is band-limited to , since a sampled signal only supports frequencies up to (see §A.4). This completes the proof of Shannon's Sampling Theorem. $$\$

A ''one-line summary of Shannon's sampling theorem is as follows:

That is, the Discrete-Time Fourier Transform of the samples is extended to plus and minus infinity by zero, and the inverse Fourier transform of that gives the original signal. The Continuous-TimeAliasing Theorem provides that the zero-padded $$\$ and $$\$ are identical, as needed.
Shannon's sampling theorem is easier to show when applied todiscrete-time sampling-rate conversion, i.e., when simple decimationof a discrete time signal is being used to reduce the sampling rate by an integer factor. In analogy with the Continuous-Time Aliasing Theorem of §A.2, the Decimation Theorem states thatdownsampling a digital signal by an integer factor produces a digital signal whose spectrum can be calculated by partitioning the original spectrum into equal blocks and then summing (aliasing) those blocks. If only one of the blocks is nonzero, then the original signal at the higher sampling rate is exactly recoverable.

<< Previous page TOC INDEX Next page >>

Shannon's Sampling Theorem

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Shannon's Sampling Theorem

Shannon's Sampling Theorem