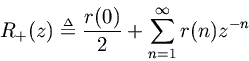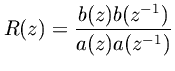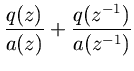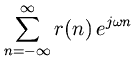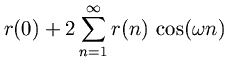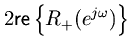02. Relation to Stochastic Processes

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Relation to Stochastic Processes

Theorem. If a stationary random process $$\$ has a rational power spectral density $$R(e^{j\$ corresponding to an autocorrelation function $$r(k)={\$ , then

is positive real.
Proof.

By the representation theorem [Astrom 1970, pp. 98-103] there exists an asymptotically stable filter which will produce a realization of $$\$ when driven by white noise, and we have $$R(e^{j\$ . We define the analytic continuation of $$R(e^{j\$ by $R(z) = H(z)H(z^{-1})$ . Decomposing into a sum ofcausal and anti-causal components gives

$$\$ $$\$ $$\$ (27)

$$\$ $$\$ (28)

where is found by equating coefficients of like powers of in

Since the poles of and are the same, it only remains to be shown that $$\$ .

Since spectral power is nonnegative, $$R(e^{j\$ for all $$\$ , and so

$$\$ $$\$ $$\$ (29)

$$\$ $$\$ (30)

$$\$ $$\$ (31)

$$\$ $$\$ (32)

$$\$