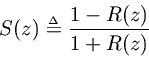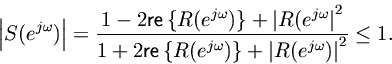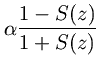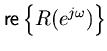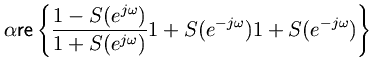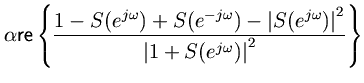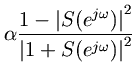03. Relation to Schur Functions

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Relation to Schur Functions

Definition. A Schur function is defined as a complex function analytic and of modulus not exceeding unity in $$\$ .

Theorem. The function

is a Schur function if and only if is positive real.
Proof.

Suppose is positive real. Then for $$\$ , $$\$ is PR. Consequently, is minimum phase which implies all roots of lie in the unit circle. Thus is analytic in $$\$ . Also,

By the maxmimum modulus theorem, takes on its maximum value in $$\$ on the boundary. Thus is Schur.
Conversely, suppose is Schur. Solving Eq. (1.2) for and taking the real part on the unit circle yields

$$\$ $$\$ $$\$ (33)

$$\$ $$\$ $$\$ (34)

$$\$ $$\$ (35)

$$\$ $$\$ (36)

$$\$ $$\$ (37)

If $$S(z)=\$ is constant, then $$R(z)=(1-\$ is PR. If is not constant, then by the maximum principle, for $$\$ . By Rouche's theorem applied on a circle of radius $$1+\$ , $$\$ , on which $$\$ , the function has the same number of zeros as the function in $$\$ . Hence, is minimum phase which implies is analytic for $$z\$ . Thus is PR. $$\$