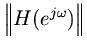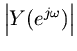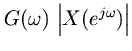12. Frequency Response

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Frequency Response

Beginning with Eq. (2.2.1), we have

where is the -transform of the filter input, is the -transform of the output signal, and is the filter transfer function.
Definition. The frequency response of a linear time-invariant digital filter is defined to be the transfer function, , evaluated on the unit circle, that is, $$H(e^{j\$ .

The frequency response is a complex-valued function of a real variable. The response at frequency Hz, for example, is $$H(e^{j2\$ , where is the sampling period in seconds.

Since every complex number can be represented as a magnitude and angle, the frequency response may be decomposed into two real-valued functions, the amplitude response and the phase response. Formally, we may define them as follows:

$$\$ $$\$ $$\$ (48)

$$\$ $$\$ $$\$ (49)

so that

Thus $$G(\$ is the magnitude (or complex modulus) of $$H(e^{j\$ , and $$\$ is the phase (or complex angle) of $$H(e^{j\$ .
Definition. The real valued function $$G(\$ in Eq. (49) is called the filter amplitude response and it specifies the amplitude gain that the filter provides at each frequency.

Definition. The function $$G^2(\$ is called the power response and it specifies the power gain at each frequency.

Definition. The real function $$\$ in Eq. (49) is thephase response and it gives the phase shift in radians that each input component sinusoid will undergo.

If the filter input and output signals are and respectively, then

$$\$ $$\$ $$\$ (50)

$$\$ $$\$ $$\$ (51)

<< Previous page TOC INDEX Next page >>

GUIDE: Elementary Digital Filter Theory - Julius O. Smith III. Frequency Response

Frequency Response