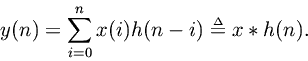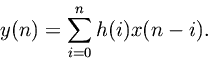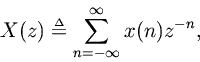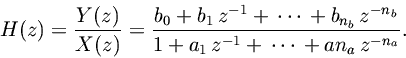11. Convolution Representation

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Convolution Representation

If is the output of an LTI filter with input and impulseresponse , then is the convolution of with ,

Since convolution is commutative (), we have also

Definition. The -transform of the discrete-time signal is defined to be

That and are transform pairs is expressed by writing or .

Theorem. The convolution theorem (Papoulis [Papoulis 1977]) states that

In words, convolution in the time domain is multiplication in the frequency domain.

Taking the -transform of both sides of Eq. (2.2.1) and applying the convolution theorem gives

where is the -transform of the filter impulse response. Thus the-transform of the filter output is the -transform of the input times the -transform of the impulse response.

Definition. The transfer function of a linear time-invariant discrete-time filter is defined to be the -transform of the impulse response .

Theorem. The shift theorem [Papoulis 1977] for -transforms states that

The general difference equation for an LTI filter appears as

			(44)
			(45)

Taking the -transform of both sides, denoting the transform by gives

			(46)
			(47)

using linearity and the shift theorem. Replacing by , by , and solving for , which equals the transfer function , yields

<< Previous page  TOC  INDEX  Next page >>