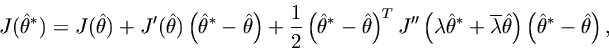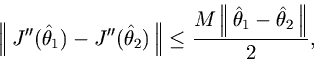NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Newton's Method
The gradient method is based on the first-order term in the Taylor expansion for
. By taking a second-order term as well and solving the quadratic minimization problem iteratively, Newton's method for functional minimization is obtained. Essentially,Newton's method requires the error surface to be close toquadratic, and its effectiveness is directly tied to the accuracy of this assumption. For most problems, the error surface can be well approximated by a quadratic form near the solution. For this reason, Newton's method tends to give very rapid (``quadratic'') convergence in the last stages of iteration.
Newton's method is derived as follows: The Taylor expansion of
about
gives
for some, where
. It is now necessary to assume that
. Differentiating with respect to
, where
is presumed to be minimum, this becomes
Solving foryields
Applying Eq. (7) iteratively, we obtain the following.Definition. Newton's method is defined by
whereis given as an initial condition.
When
, the answer is obtained after the first iteration. In particular, when the error surface
is a quadratic form in
, Newton's method produces
in one iteration, i.e.,
for every
.
For Newton's method, there is the following general result on the existence of a critical point (i.e. a point at which the gradient vanishes) within a sphere of a Banach space.
Theorem. (Kantorovich) Let
be a point in
for which
exists, and set
Letdenote the sphere
. Set
. If there exists a number
such that
forin
, and such that
, then
for some
in
, and the Newton sequence Eq. (7) converges to it. Furthermore, the rate of convergence is quadratic, satisfying
Proof. See Goldstein [Goldstein 1967], p. 143.