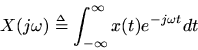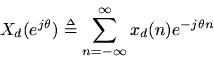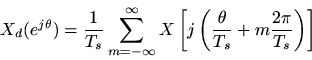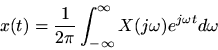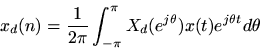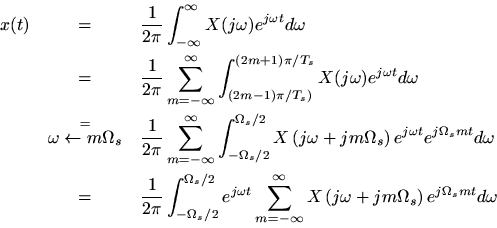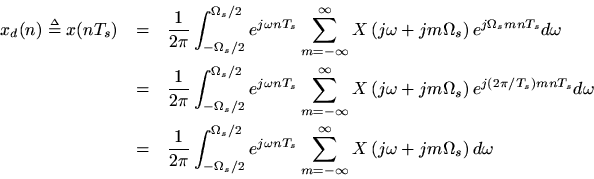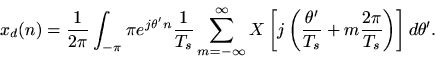NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Aliasing of Sampled Continuous-Time SignalsThis section quantifies aliasing in the general case. This result is then used in the proof of Shannon's Sampling Theorem in the next section.
It is well known that when a continuous-time signal contains energy at a frequency higher than half the sampling rate
, then sampling at
samples per second causes that energy to alias to a lower frequency. If we write the original frequency as
, then the new aliased frequency is
, for
. This phenomenon is also called ''folding'', since
is a ''mirror image'' of
about
. As we will see, however, this is not a fundamental description of aliasing, as it only applies to real signals. For general (complex) signals, it is better to regard the aliasing due to sampling as a summation over all spectral ''blocks'' of width
.
Theorem. (Continuous-Time Aliasing Theorem) Let
denote any continuous-time signal having a Fourier Transform (FT)
Let
denote the samples ofat uniform intervals of
seconds, and denote its Discrete-Time Fourier Transform (DTFT) by
Then the spectrumof the sampled signal
is related to the spectrum
of the original continuous-time signal
by
The terms in the above sum forare called aliasing terms. They are said to alias into the base band
. Note that the summation of a spectrum with aliasing components involves addition of complex numbers; therefore, aliasing components can be removed only if both their amplitudeand phase are known.
Proof. Writing
as an inverse FT gives
Writingas an inverse DTFT gives
wheredenotes the normalized discrete-time frequency variable.
The inverse FT can be broken up into a sum of finite integrals, each of length
, as follows:
Let us now sample this representation forat
to obtain
sinceand
are integers. Normalizing frequency as
yields
Since this is formally the inverse DTFT ofwritten in terms of
, the result follows.