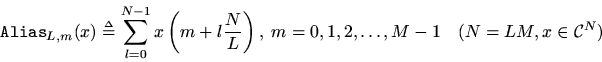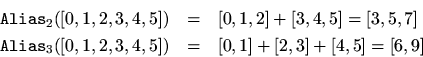Alias Operator

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Alias Operator

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Alias Operator

Aliasing occurs when a signal is undersampled. If the signalsampling rate $f_s$ is too low, we get frequency-domain aliasing.

The topic of aliasing normally arises in the context of sampling a continuous-time signal. Shannon's Sampling Theorem says that we will have no aliasing due to sampling as long as the sampling rate is higher than twice the highest frequency present in the signal being sampled.

In this chapter, we are considering only discrete-time signals, in order to keep the math as simple as possible. Aliasing in this context occurs when a discrete-time signal is decimated to reduce its sampling rate. You can think of continuous-time sampling as the limiting case for which the starting sampling rate is infinity.

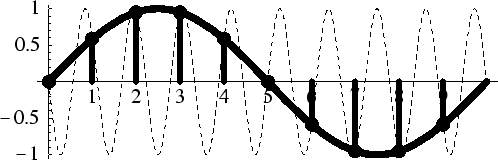
An example of aliasing is shown in Fig. 8.9. In the figure, the high-frequency sinusoid is indistinguishable from the lower frequency sinusoid due to aliasing. We say the higher frequencyaliases to the lower frequency. Undersampling in the frequency domain gives rise totime-domain aliasing. If time or frequency is not specified, the term ''aliasing'' normally means frequency-domain aliasing.

Figure 8.9:Example of aliasing due to undersampling in time.
\

The aliasing operator is defined by

\

Like the $\ operator, the $\ operator maps a length$N=LM$ signal down to a length $M$ signal. The way to think of it is to partition the original $N$ samples in to $L$ blocks of length $M$, with the first block extending from sample $0$ to sample $M-1$, the second block from $M$ to $2M-1$, etc. Then just add up the blocks. This process is called aliasing. If the original signal $x$ is a time signal, it is called time-domain aliasing; if it is a spectrum, we call it frequency-domain aliasing, or just aliasing. Note that aliasing is not invertible. Once the blocks are added together, it is not possible to recover the original blocks, in general.

For example,

\


The alias operator is used to state the Fourier theorem

\

That is, when you decimate a signal by the factor $L$, its spectrum is aliased by the factor $L$.
Figure:Illustration of aliasing in the frequency domain. a) $\ from Fig. 8.7c. b) First half of the original unit circle ($0$ to $\) wrapped around the new, smaller unit circle (which is magnified to the original size). c) Second half ($\ to $2\), also wrapped around the new unit circle. d) Overlay of components to be summed. e) Sum of components (the aliased spectrum). f) Both sum and overlay.
\

Figure 8.10 shows the result of $\ applied to $\from Fig. 8.7c. Imagine the spectrum of Fig. 8.10a as being plotted on a piece of paper rolled to form a cylinder, with the edges of the paper meeting at $z=1$ (upper right corner of Fig. 8.10a). Then the $\ operation can be simulated by rerolling the cylinder of paper to cut its circumference in half. That is, reroll it so that at every point, two sheets of paper are in contact at all points on the new, narrower cylinder. Now, simply add the values on the two overlapping sheets together, and you have the $\ of the original spectrum on the unit circle. To alias by $3$, we would shrink the cylinder further until the paper edges again line up, giving three layers of paper in the cylinder, and so on.

Figure 8.10b shows what is plotted on the first circular wrap of the cylinder of paper, and Fig. 8.10c shows what is on the second wrap. These are overlaid in Fig. 8.10d and added together in Fig. 8.10e. Finally, Fig. 8.10f shows both the addition and the overlay of the two components. We say that the second component (Fig. 8.10c) ''aliases'' to new frequency components, while the first component (Fig. 8.10b) is considered to be at its original frequencies. If the unit circle of Fig. 8.10a covers frequencies$0$ to $f_s$, all other unit circles (Fig. 8.10b-c) cover frequencies $0$ to $f_s/2$.

In general, aliasing by the factor $K$ corresponds to a sampling-rate reduction by the factor $K$. To prevent aliasing when reducing the sampling rate, an anti-aliasing lowpass filter is generally used. The lowpass filter attenuates all signal components at frequencies outside the interval $[-f_s/(2K),f_s/(2K)]$. If they are not filtered out, they will alias, and aliasing is generally non-invertible.

Conceptually, the unit circle is reduced by $\ to a unit circlehalf the original size, where the two halves are summed. The inverse of aliasing is then ''repeating'' which should be understood as increasing the unit circle circumference using ''periodic extension'' to generate ''more spectrum'' for the larger unit circle. In the time domain,decimation is the inverse of the stretch operator. All of these relationships are precise only for integerstretch/decimation/aliasing/repeat factors; in continuous time, the restriction to integer factors is removed, and we obtain the (simpler) similarity theorem (proved in §8.10).

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy