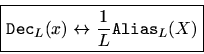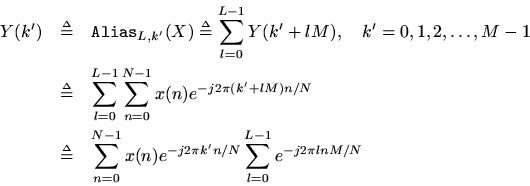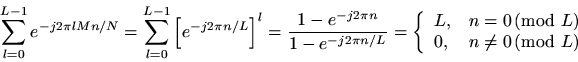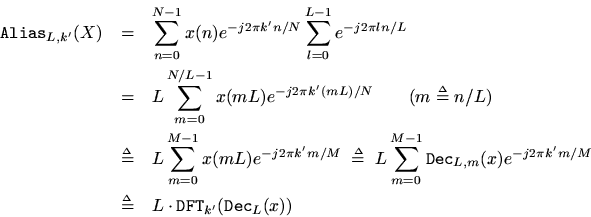Decimation Theorem (Aliasing Theorem)

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Decimation Theorem (Aliasing Theorem)

Theorem: For all ,

Proof: Let denote the frequency index in the aliased spectrum, and let . Then is length , where is the decimation factor. We have

Since , the sum over becomes

using the closed form expression for a geometric series derived earlier. We see that the sum over effectively samples every samples. This can be expressed in the previous formula by defining which ranges only over the nonzero samples:

Since the above derivation also works in reverse, the theorem is proved.

Here is an illustration of the Decimation Theorem in Matlab:

>> N=4;
>> x = 1:N;
>> X = fft(x);
>> x2 = x(1:2:N);
>> fft(x2)                         % FFT(Decimate(x,2))

ans =

 4    -2

>> (X(1:N/2) + X(N/2 + 1:N))/2     % (1/2) Alias(X,2)

ans =

4.0000   -2.0000</pre></p><p>An illustration of aliasing in the frequency domain is shown in

Fig. 8.10.

<< Previous page  TOC  INDEX  Next page >>