Constructive and Destructive Interference of Sinusoids

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Constructive and Destructive Interference of Sinusoids

Sinusoidal signals are analogous to monochromatic laser light. You might have seen ''speckle'' associated with laser light, caused by destructive inteference of multiple reflections of the light beam. In a room, the same thing happens with sinusoidal sound. For example, play a simple sinusoidal tone (e.g., ''A-440'' which is a sinusoid at frequency Hz) and walk around the room with one ear plugged. If the room is reverberant you should be able find places where the sound goes completely away due to destructive interference. In between such places (which we call ''nodes'' in the soundfield), there are ''antinodes'' at which the sound is louder by 6 dB (amplitude doubled) due to constructive interference. In a diffuse reverberant soundfield, the distance between nodes is on the order of a wavelength (the ''correlation distance'' within the random soundfield).

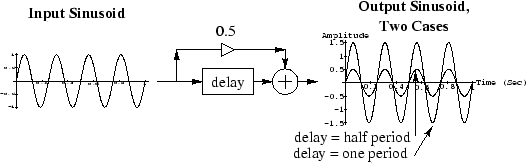
The way reverberation produces nodes and antinodes for sinusoids in a room is illustrated by the simple comb filter.^5.2 There is also shown in Fig. 5.3. A unit-amplitude sinusoid is present at the input, and the output must also be sinusoidal, since the comb filter is linear and time-invariant. The feedforward path of the comb filter has a gain of , and the delay is one period in one case and half a period in the other. With the delay set to one period, the unit amplitude sinusoid coming out of the delay line constructively interferes with the amplitude sinusoid from the feed-forward path, and the output amplitude is therefore . In the other case, with the delay set to half period, the unit amplitude sinusoid coming out of the delay line destructively interferes with the amplitude sinusoid from the feed-forward path, and the output amplitude therefore drops to .

Figure 5.3:A comb filter with a sinusoidal input.

comb-filter

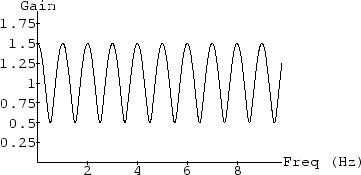
Consider a fixed delay of seconds for the delay line. Constructive interference happens at all frequencies for which an exact integernumber of periods fits in the delay line, i.e., , or, for . On the other hand, destructive interference happens at all frequencies for which number of periods in the delay line is an integer plus a half, i.e., etc., or, , for . It is quick to verify that frequencies of constructive interference alternate with frequencies of destructive interference, and therefore the amplitude response of the comb filter (a plot of gain versus frequency) looks as shown in Fig. 5.4.

Figure 5.4:Comb filter amplitude response when the delay is sec.

The ampitude response of a comb filter has a ''comb'' like shape, hence the name.^5.3 Note that if the feedforward gain is increased from to , the comb-filter gain ranges between (complete cancellation) and . Negating the feedforward gain inverts the gain curve, placing a minumum at dc^5.4 instead of a peak.

<< Previous page  TOC  INDEX  Next page >>