Stretch Operator

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Stretch Operator

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>


Stretch Operator

Unlike all previous operators, the $\ operator maps a length $N$ signal to a length $M\ signal, where $L$ and $N$ are integers. We use ''$m$'' instead of ''$n$'' as the time index to underscore this fact.

Figure:Illustration of $\.
\



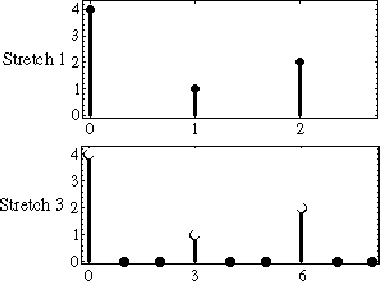
Definition: A stretch by factor $L$ is defined by

\

Thus, to stretch a signal by the factor $L$, insert $L-1$ zeros between each pair of samples. An example of a stretch by factor three is shown in Fig. 8.4. The example is
\

The stretch operator is used to describe and analyze upsampling, i.e., increasing the sampling rate by an integer factor.

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy