NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Example 5: Use of the Blackman Window
Now let's apply this window to the sinusoidal data:
% Use the Blackman window on the sinusoid data xw = [w .* cos(2*pi*n*f*T),zeros(1,(zpf-1)*N)]; % windowed, zero-padded data X = fft(xw); % Smoothed, interpolated spectrum
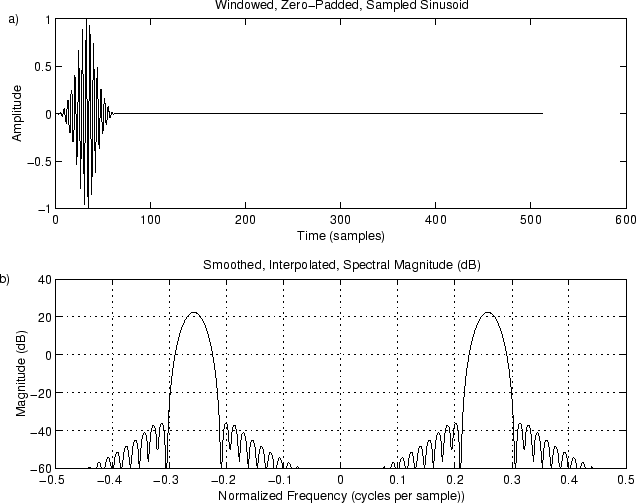
% Plot time data figure(6); subplot(2,1,1); plot(xw);
title(‘Windowed, Zero-Padded, Sampled Sinusoid’); xlabel(‘Time (samples)’); ylabel(’Amplitude’); text(-50,1,‘a)’); hold off;
% Plot spectral magnitude in the best way spec = 10*log10(conj(X).X); % Spectral magnitude in dB spec = max(spec,-60ones(1,nfft)); % clip to -60 dB subplot(2,1,2); plot(fninf,fftshift(spec),’-’); axis([-0.5,0.5,-60,40]); grid; title(‘Smoothed, Interpolated, Spectral Magnitude (dB)’); xlabel(‘Normalized Frequency (cycles per sample))’); ylabel(‘Magnitude (dB)’); text(-.6,40,‘b)’); print -deps eps/xw.eps;